堆 | Homeward

经过努力，最值总会冒上来的！

一、定义#

通常情况下，使用列表储存堆，堆树是完全二叉树，而二项堆和斐波那契堆不属于二叉树；
堆树中某个节点的值总是不大于或不小于其孩子节点的值；
堆树中每个节点的子树都是堆树。

当父节点的键值总是大于或等于任何一个子节点的键值时为最大堆。当父节点的键值总是小于或等于任何一个子节点的键值时为最小堆。本文以最大堆作为例子，最小堆类似。

二、堆的建立#

堆的建立并不建立一个新的树，而是对数组进行原地改动，第一个数（index=0）为完全二叉树的 level 0，即根，第二个数和第三个数为 level 1，以此类推。

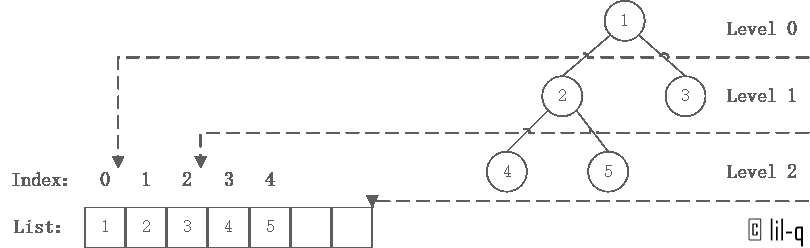
由于数组是升序数组，我们直接得到了最小堆。但是如果要进行升序排序，算法上需要建立最大堆。也就是说，当原数组是升序时，堆排序算法遇到了最坏情况。本文也以这种情况作为例子。

nums=[1,2,3,4,5]

2.1 堆的维护#

上图的根节点是 1，小于子节点，那么这显然违反了最大堆的性质，这时候需要让该元素在最大堆中逐级下降，维护最大堆的性质。处理一次维护的代码如下：

def adjust_heap(idx, max_len,nums):
    left = 2 * idx + 1
    right = 2 * idx + 2
    max_loc = idx
    if left < max_len and nums[max_loc] < nums[left]:
        max_loc = left
    if right < max_len and nums[max_loc] < nums[right]:
        max_loc = right
    if max_loc != idx:
        nums[idx], nums[max_loc] = nums[max_loc], nums[idx]
        adjust_heap(max_loc, max_len,nums)

2.2 建立最大堆#

自底向上处理，因为数组 list[n//2, n] 中的所有元素都在堆树的叶节点中，因此可以看成只包含一个元素的堆，无需维护。其中 n = len(list)；
从 index = n//2 - 1 开始，直到 index = 0，对每一个节点或根进行一次维护。

一次维护并不是最多只交换一次，而是交换到某节点满足最大堆条件或者 index >= n 为止。

heapflow

def build_heap(nums):    
    n = len(nums)
    for i in range(n // 2 - 1, -1, -1):
        adjust_heap(i, n,nums)
    return nums
heap=build_heap(nums)
print("heap:",heap)
#输出：heap: [5, 4, 3, 1, 2]

三、最大堆中插入节点#

最大堆的插入节点的思想就是先在堆的最后添加一个节点，也就是在 list.append()，然后沿着堆树上升。跟最大堆的初始建立过程大致相同。

def heap_insert(heap,num):
    heap=heap+[num]
    n=len(heap)
    i=n-1
    while i>0 and heap[(i-1)//2]<num:
        heap[i]=heap[(i-1)//2]
        i=(i-1)//2
    heap[i]=num
    return heap
heap=heap_insert(heap,6)
print("heapIns:",heap)
#输出：heapIns: [6, 4, 5, 1, 2, 3]

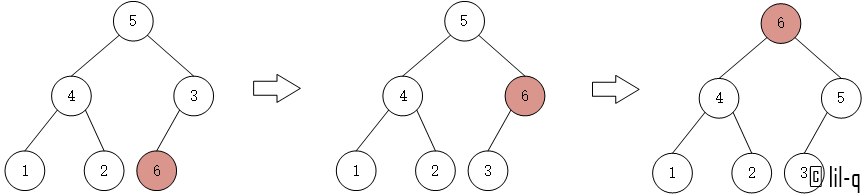
charu

四、最大堆节点的删除#

对一个节点的删除就是交换该节点和最后一个叶子节点的值，并从该节点开始一次 adjust_heap()：

def heap_delete(heap,idx):
    n=len(heap)
    heap[idx],heap[-1]=heap[-1],heap[idx]
    adjust_heap(idx, n - 1,heap)
    heap.pop()
    return heap
heap=heap_delete(heap,0)
print("heapDel:",heap)
#输出：heapDel: [5, 4, 3, 1, 2]

五、堆排序#

特殊地，当我们交换根和最后一个叶子节点时，就能够提出最大值，并且存放在 index = -1 的位置。然后再对前 n - 1 个数组成的最大堆进行该处理，以此类推，最终完成堆排序。

def heap_sorted(heap):
    for i in range(1, len(heap)):
        heap[0], heap[-i] = heap[-i], heap[0]
        adjust_heap(0, n - i, heap)
    return heap
heapSort=heap_sorted(heap)
print("heapSort:",heapSort)
#输出：heapSort: [1, 2, 3, 4, 5]

参考#

top K