排序算法 | Homeward

十种排序算法的 python 实现及复杂度分析

分类#

评价排序算法的几个指标：

时间复杂度：包括平均时间复杂度、最坏时间复杂度和最好时间复杂度。一般而言，好的性能是 $O(nlog_2n)$，坏的性能是 $O(n^2)$。对于一个排序理想的性能是 $O(n)$，但平均而言不可能达到。基于比较的排序算法对大多数输入而言至少需要 $O(nlog_2n)$。
空间复杂度：内存使用量
稳定性：稳定排序算法会让原本有相等键值的纪录维持相对次序。也就是如果一个排序算法是稳定的，当有两个相等键值的纪录 R 和 S，且在原本的列表中 R 出现在 S 之前，在排序过的列表中 R 也将会是在 S 之前。
依据排序的方法：插入、交换、选择、合并等等。

本文介绍了以下几种排序，推荐可视化网站 visualgo ，下文代码都采用数组作为输入。

排序方法	平均时间复杂度	最坏时间复杂度	最好时间复杂度	空间复杂度	稳定性
冒泡排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	稳定
选择排序	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	不稳定
插入排序	$O(n^2)$	$O(n^2)$	$O(n)$	$O(1)$	稳定
堆排序	$O(nlog_2n)$	$O(nlog_2n)$	$O(nlog_2n)$	$O(1)$	不稳定
归并排序	$O(nlog_2n)$	$O(nlog_2n)$	$O(nlog_2n)$	$O(n)$	稳定
快速排序	$O(nlog_2n)$	$O(n^2)$	$O(nlog_2n)$	$O(log_2n)$	不稳定
希尔排序	$O(n^{1.3})$	$O(n^2)$	$O(n)$	$O(1)$	不稳定
计数排序	$O(n+m)$	$O(n+m)$	$O(n+m)$	$O(n+m)$	稳定
基数排序	$O(n*k)$	$O(n*k)$	$O(n*k)$	$O(n+k)$	稳定
桶排序	$O(n+k)$	$O(n^2)$	$O(n)$	$O(n+k)$	稳定

均按从小到大排列
k 代表数值中的 “数字” 个数
n 代表数据规模
m 代表数据的最大值减最小值

冒泡排序#

数据分区：（无序区，有序区）。
从无序区透过交换找出最大元素放到有序区前端。

冒泡排序

流程

比较相邻的元素，如果第一个比第二个大，就交换他们两个；
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数；
针对所有的元素重复以上的步骤，除了最后一个；
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

冒泡流程

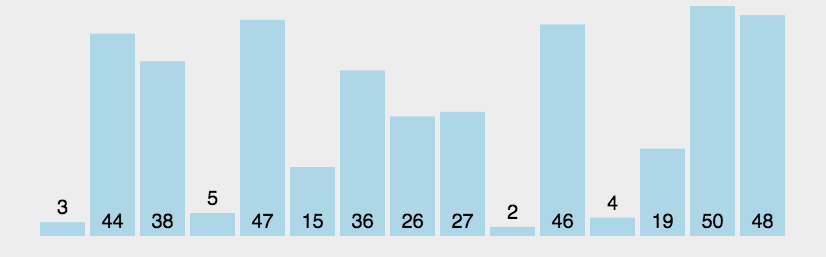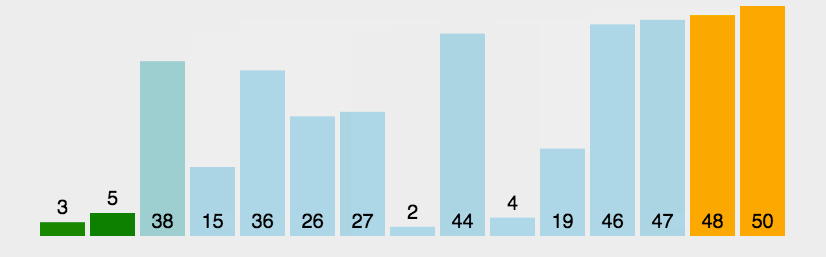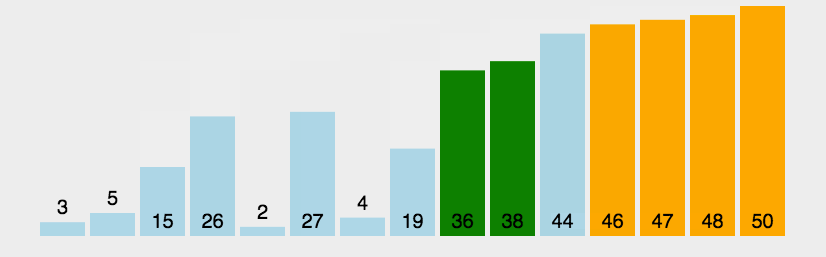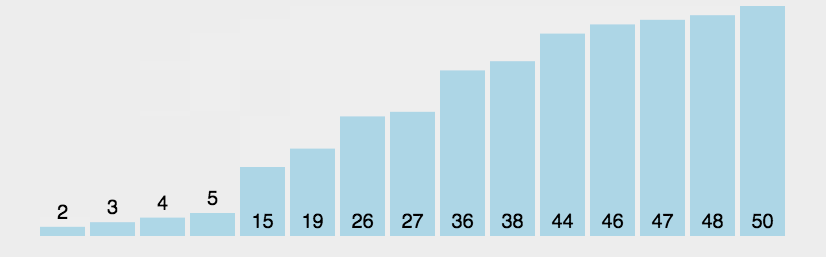
代码

def bubble_sorted(nums):
    size = len(nums)
    for i in range(size-1):
        for j in range(size-1-i):
            if nums[j] > nums[j+1]:
                nums[j],nums[j+1]=nums[j+1],nums[j]
    return nums

但是，该算法的最优时间复杂度并不是 $O(n)$，而是 $O(n^2)$ [5] 。需改写才能实现最优理想状态：

def bubble_sorted(nums):
    size = len(nums)
    for i in range(size-1):
        didSwap=False
        for j in range(size-1-i):
            if nums[j] > nums[j+1]:
                nums[j],nums[j+1]=nums[j+1],nums[j]
                didSwap=True
        if didSwap==False:
            return
    return nums

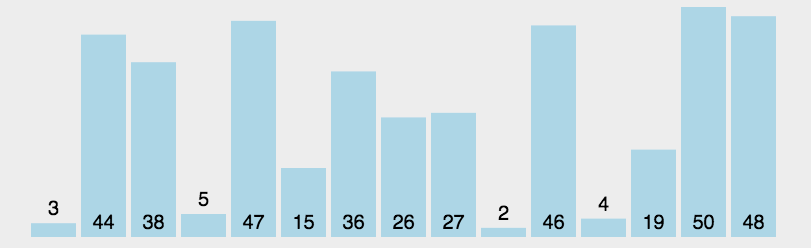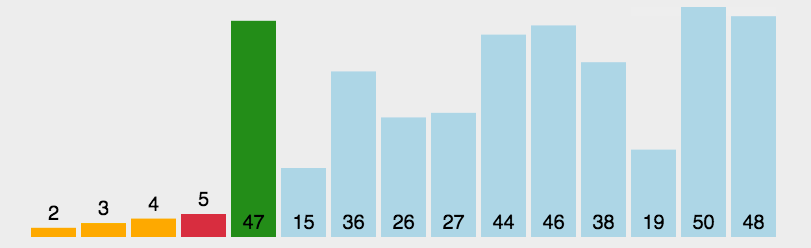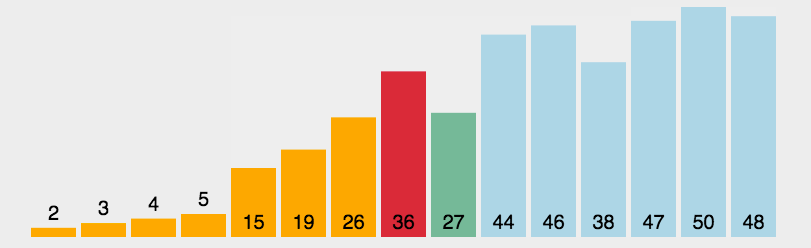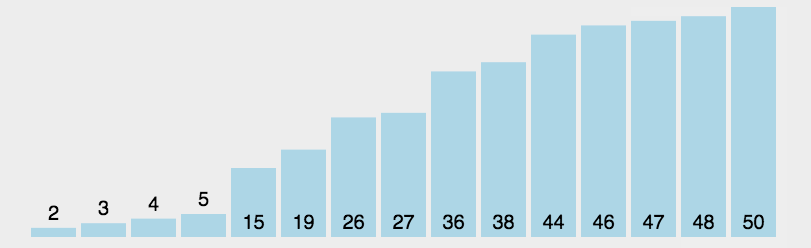
选择排序#

数据分区：（有序区，无序区）。
在无序区里找一个最小的元素跟在有序区的后面。对数组：比较得多，换得少。

选择排序

流程

初始状态：无序区为 R[1..n]，有序区为空；
第 i 趟排序（i = 1, 2, 3, …, n-1）开始时，当前有序区和无序区分别为 R[1, …, i - 1] 和 R[i, …, n]。该趟排序从当前无序区中选出关键字最小的记录 R[k]，将它与无序区的第 1 个记录R交换，使 R[1, …, i] 和 R[i + 1, …, n] 分别变为记录个数增加 1 个的新有序区和记录个数减少 1 个的新无序区；
n - 1 趟结束，数组有序化了。

选择流程

代码

def selection_sorted(nums):
    size = len(nums)
    for i in range(size-1):
        min_index = i
        for j in range(i, size):
            if nums[j] < nums[min_index]:
               min_index = j
        nums[i], nums[min_index] = nums[min_index], nums[i]
    return nums

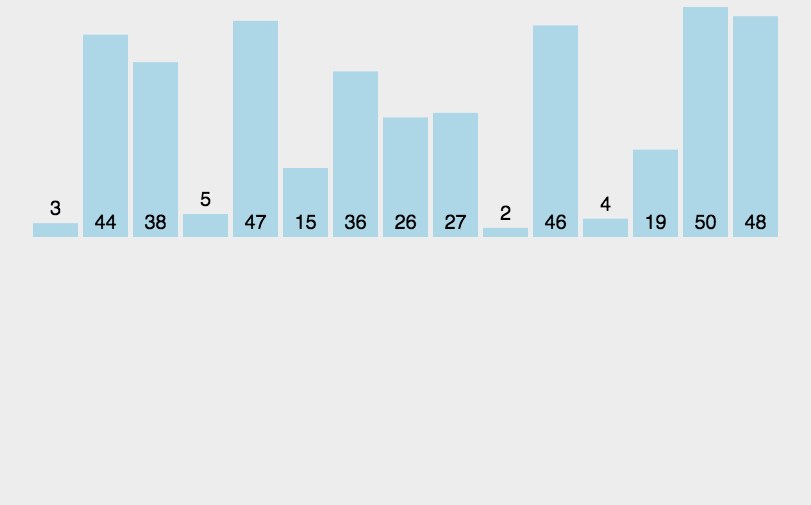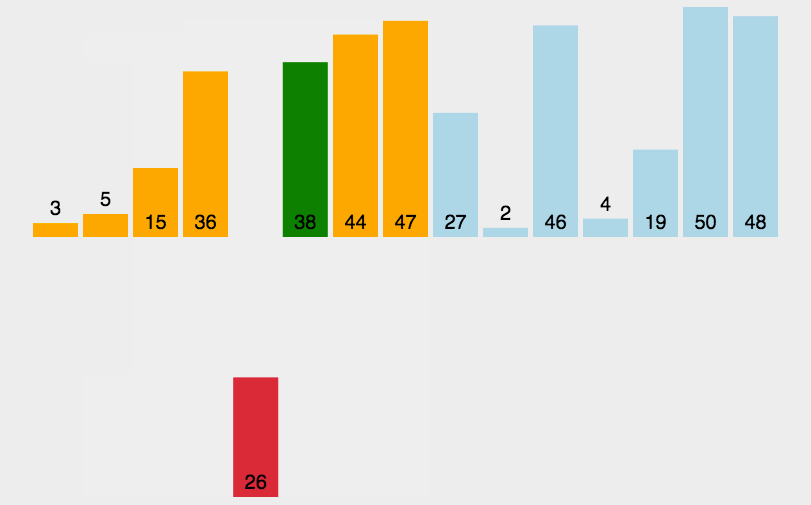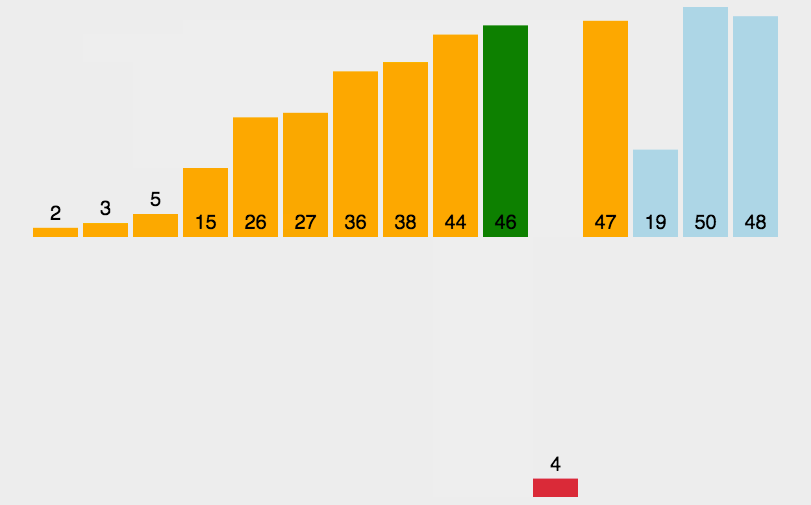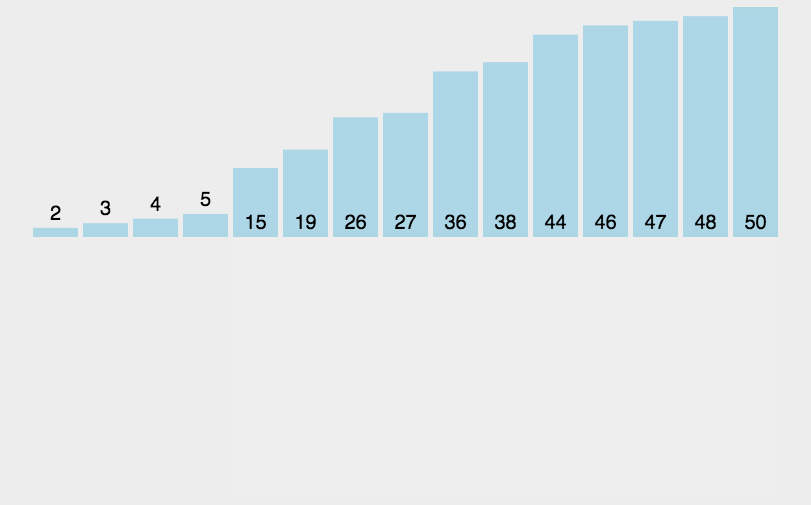
插入排序#

数据分区：（有序区，无序区）。
把无序区的第一个元素插入到有序区的合适的位置。对数组：比较得少，换得多。

插入排序

流程

从第一个元素开始，该元素可以认为已经被排序；
取出下一个元素，在已经排序的元素序列中从后向前扫描；
如果该元素（已排序）大于新元素，将该元素移到下一位置；
重复步骤 3，直到找到已排序的元素小于或者等于新元素的位置；
将新元素插入到该位置后；
重复步骤 2 ~ 5。

插入流程

代码

def insertion_sorted(nums):
	size = len(nums)
	for i in range(1,size):
		cur_num=nums[i]
		pre_index=i-1
		while nums[pre_index]>cur_num and pre_index>=0:
			nums[pre_index+1]=nums[pre_index]
			pre_index-=1
		nums[pre_index+1]=cur_num
	return nums

堆排序#

数据分区：（最大堆，有序区）。
从堆顶把根卸出来放在有序区之前，再恢复堆。关于堆

heap

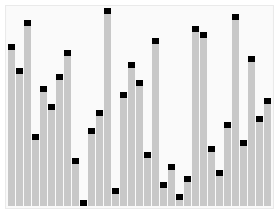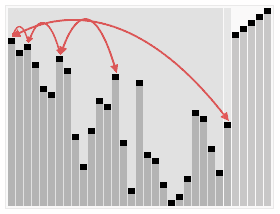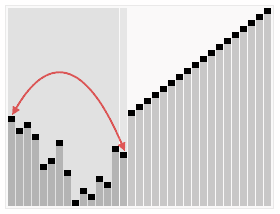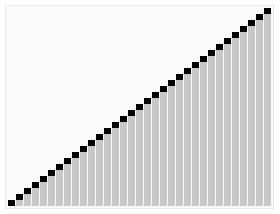
流程

最大堆调整（Max Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点；
创建最大堆（Build Max Heap）：将堆中的所有数据重新排序；
堆排序（HeapSort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算。

代码

def heap_sorted(nums):
    # 调整最大堆         
    def adjust_heap(idx, max_len):
        left = 2 * idx + 1
        right = 2 * idx + 2
        max_loc = idx
        if left < max_len and nums[max_loc] < nums[left]:
            max_loc = left
        if right < max_len and nums[max_loc] < nums[right]:
            max_loc = right
        if max_loc != idx:
            nums[idx], nums[max_loc] = nums[max_loc], nums[idx]
            adjust_heap(max_loc, max_len)  
    # 建堆
    n = len(nums)
    for i in range(n // 2 - 1, -1, -1):
        adjust_heap(i, n)
    # 排序
    for i in range(1, n):
        nums[0], nums[-i] = nums[-i], nums[0]
        adjust_heap(0, n - i)
    return nums

归并排序#

把数据分为两段，从两段中逐个选最小的元素移入新数据段的末尾。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

merge

流程

把长度为 n 的输入序列分成两个长度为 n/2 的子序列；
对这两个子序列分别采用归并排序；
将两个排序好的子序列合并成一个最终的排序序列。

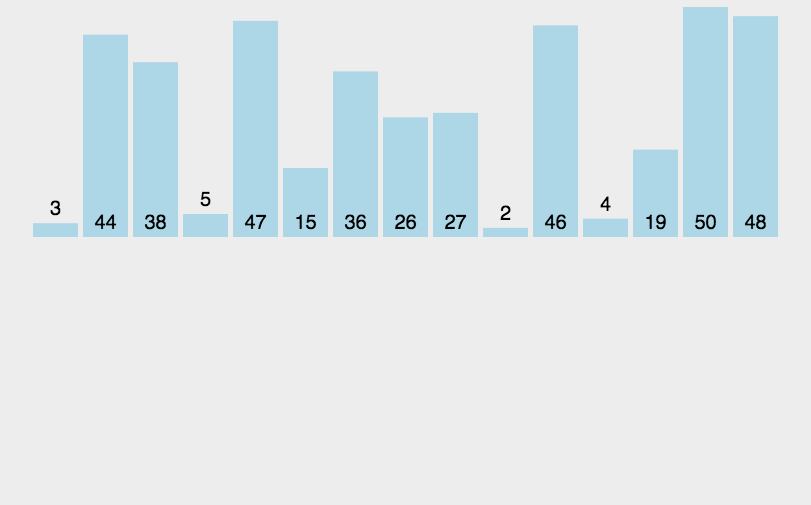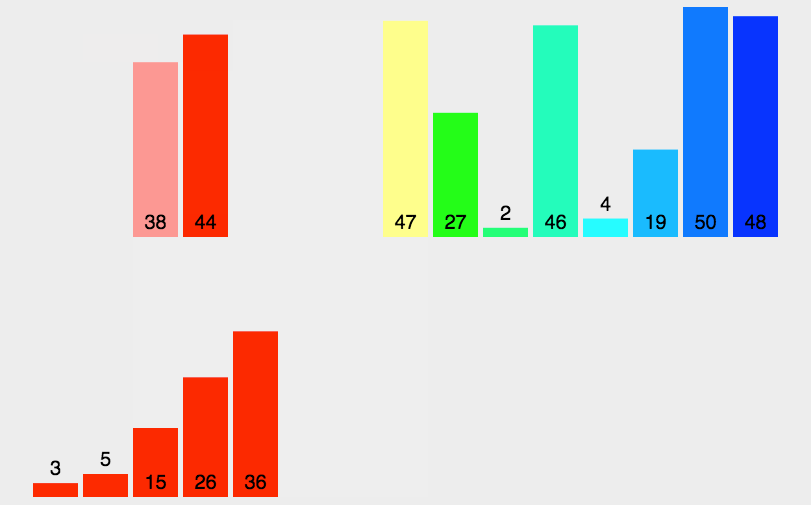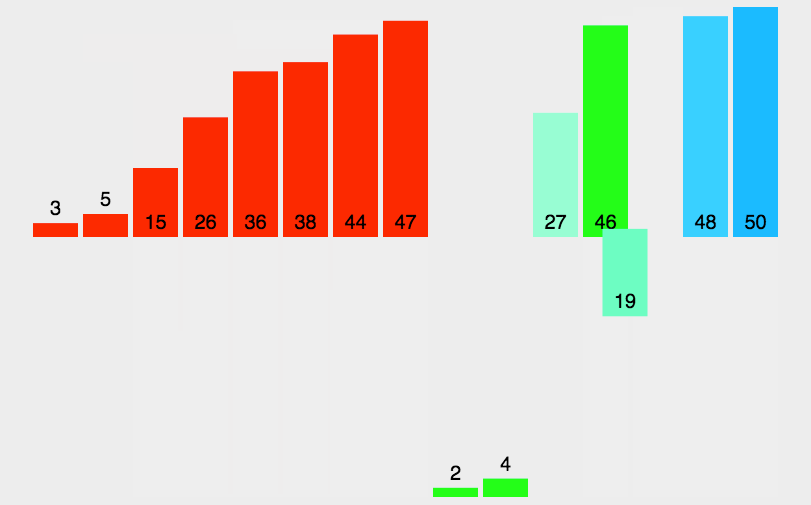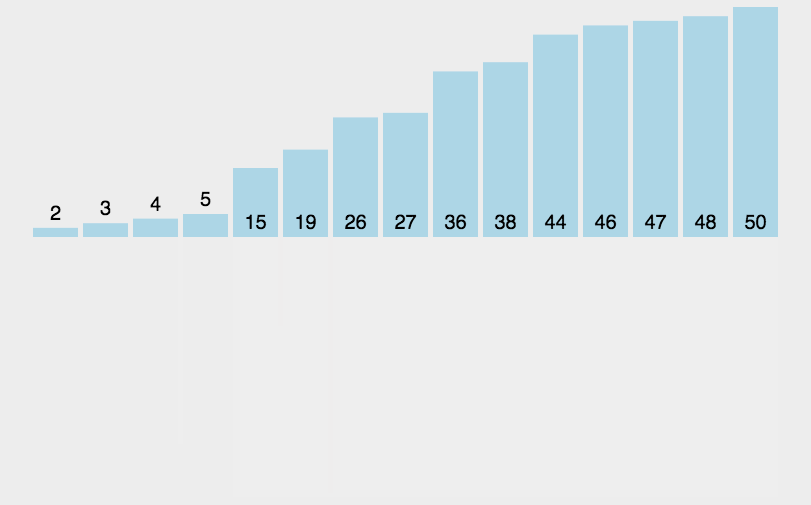
mergef

代码

递归法（Top-down）：

def merge(left, right):
    result = []
    while left and right:
        if left[0] <= right[0]:
            result.append(left.pop(0))
        else:
            result.append(right.pop(0))
    if left:
        result += left
    if right:
        result += right
    return result

def merge_sort(L):
    if len(L) <= 1:
        return L
    mid = len(L) // 2
    left = L[:mid]
    right = L[mid:]
    left = merge_sort(left)
    right = merge_sort(right)
    return merge(left, right)

时间复杂度是 O(nlogn)，归并的空间复杂度为临时的数组和递归时压入栈的数据占用的空间：n + logn，所以空间复杂度为: O(n) [6] 。

迭代法（Bottom-up）

重写 merge()，实现 $O(1)$：

def merge_iter(nums,l1,l2,r2):
	r1=l2-1
	while r1>=l1 and r2>=l2:
		if nums[r1]>nums[r2]:
			tmp=nums[r2] # 暂存较小值
			nums[r2]=nums[r1]
			tmp_r1=r1-1
             # 将前半数组的大于tmp的值后移一个单位
			while nums[tmp_r1]>tmp and tmp_r1>=l1: 
				nums[tmp_r1+1]=nums[tmp_r1]
				tmp_r1-=1
			nums[tmp_r1+1]=tmp
		r2-=1

这里参考了leetcode 88.合并两个有序数组，采用双指针从后往前合并两个有序数组（其实也就是一个数组切片的前一半和后一半），实现了空间复杂度 O(1)。

merge

方法一：使用生成器

# 生成器产生2的幂
def powerOfTwo(max):
	x=1
	while x<=max:
		yield x
		x*=2
# 方法一：用生成器产生1，2，4，8...
def merge_sorted_iter(nums):
	sortedList=[]
	n=len(nums)
	for i in powerOfTwo(n):
	 	for j in range(0,n,i*2):
	 		merge_iter(nums,j,min(j+i,n-1),min(j+2*i-1,n-1))
	return nums

方法二：使用位运算

# 方法二：用位操作产生1，2，4，8...
def msi(nums):
	length = len(nums)
	step = 1
    # 步长为1,2,4,8，...，一直合并下去
	while step <= length:
		offset = step << 1
		for index in range(0, length, offset):
			merge_iter(nums, index, min(index+step, length-1), min(index+offset-1, length-1))
		step = offset

时间复杂度是 $O(nlog^2n)$，空间复杂度为: $O(1)$。

快速排序#

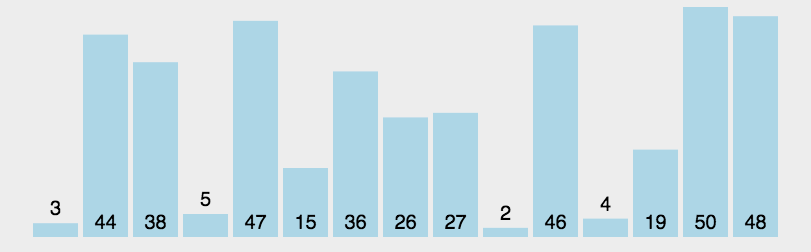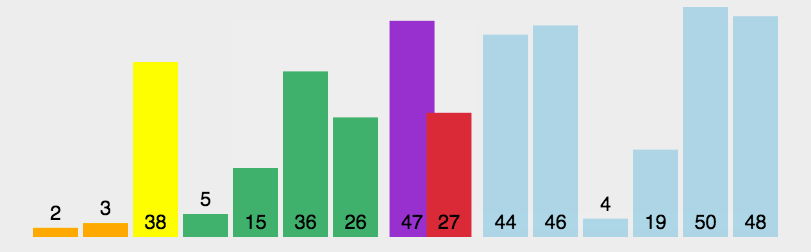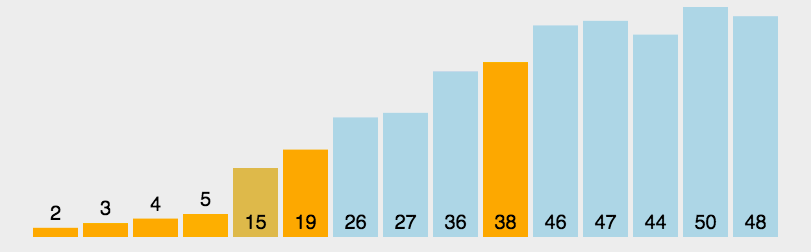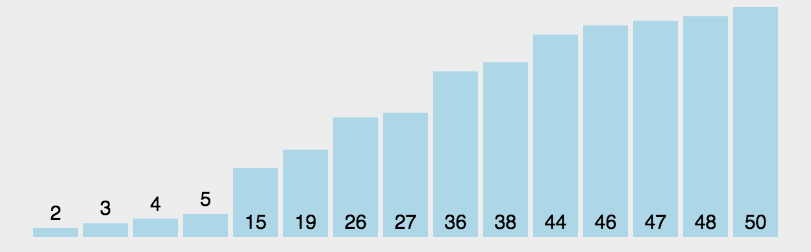
数据分区：（小数，基准元素，大数）。在区间中随机挑选一个元素作基准，将小于基准的元素放在基准之前，大于基准的元素放在基准之后，再分别对小数区与大数区进行排序。

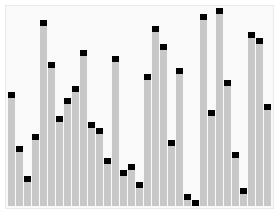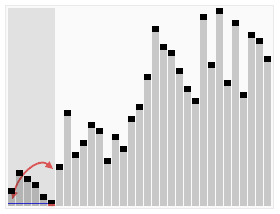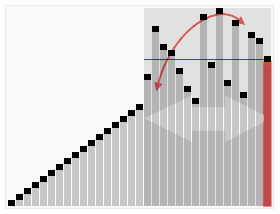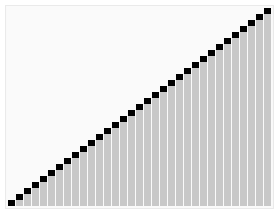
quick

流程

从数列中挑出一个元素，称为 “基准”（pivot）；
重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

quicks

代码

import random
def quick_sorted(nums):
    if len(nums) <= 1:
        return nums
    left, right, mid = [], [], []
    pivot = random.choice(nums)
    for num in nums:
        if num == pivot:
            mid.append(num)
        elif num < pivot:
            left.append(num)
        else:
            right.append(num)
    return quick_sorted(left) + mid + quick_sorted(right)

需要 ${\Omega (n)}$ 的额外存储空间，也就跟归并排序一样不好。额外需要的存储空间，在实际实现时，也会极度影响速度和缓存的性能。下面是原地排序的代码，平均可以达到 $O(\log n)$ 的空间复杂度 [7] 。

def quick_sorted_inp(nums, first, last):
    if first >= last:
        return
    mid_value = nums[first]
    low = first
    high = last
    while low < high:
        while low < high and nums[high] >= mid_value:
            high -= 1
        nums[low] = nums[high]
        while low < high and nums[low] < mid_value:
            low += 1
        nums[high] = nums[low]
    nums[low] = mid_value
    quick_sorted_inp(nums, first, low-1)
    quick_sorted_inp(nums, low+1, last)

希尔排序#

也称递减增量排序算法，是插入排序的一种更高效的改进版本。希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率；
但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

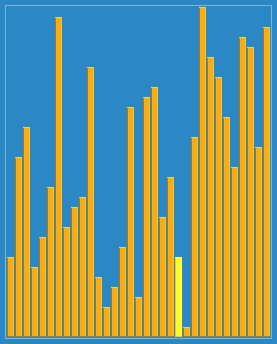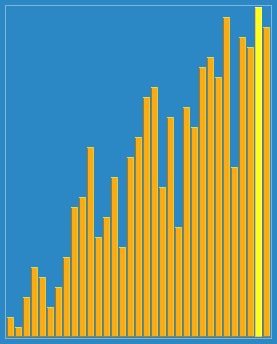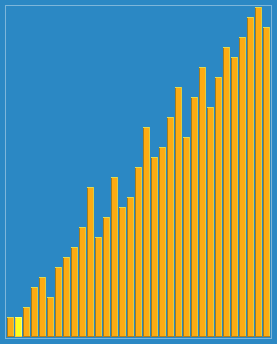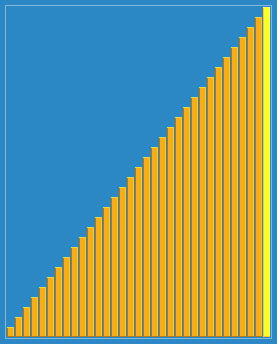
shell

流程

选择一个增量序列 $t_1$，$t_2$，…，$t_k$，其中 $t_i$ > $t_j$，$t_k$ = 1；
按增量序列个数 k，对序列进行 k 趟排序；
每趟排序，根据对应的增量 $t_i$，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

代码

def shell_sorted(nums):
    n = len(nums)
    # 初始步長，理论上只要最终步长为1任何步长序列都可以工作
    gap = n // 2
    while gap > 0:
        for i in range(gap, n):
            # 每个步長進行插入排序
            temp = nums[i]
            j = i
            # 插入排序
            while j >= gap and nums[j - gap] > temp:
                nums[j] = nums[j - gap]
                j -= gap
            nums[j] = temp
        # 得到新的步長
        gap = gap // 2
    return nums

实际上使用 1，2，4，8… 的增量序列有时会在 gap = 1 时浪费很多时间，Mark Allen Weiss 指出，最好的增量序列是 Sedgewick 提出的 (1, 5, 19, 41, 109,…)，该序列的项来自 9 * 4^i - 9 * 2^i + 1 和 4^i - 3 * 2^i + 1 这两个算式。使用 Sedgewick增量的希尔排序的完整C语言程序

计数排序#

计数排序不是基于比较的排序算法，其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

流程

找出待排序的数组中最大和最小的元素；
统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项；
对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）；
反向填充目标数组：将每个元素 i 放在新数组的第 C(i) 项，每放一个元素就将 C(i) 减去 1。

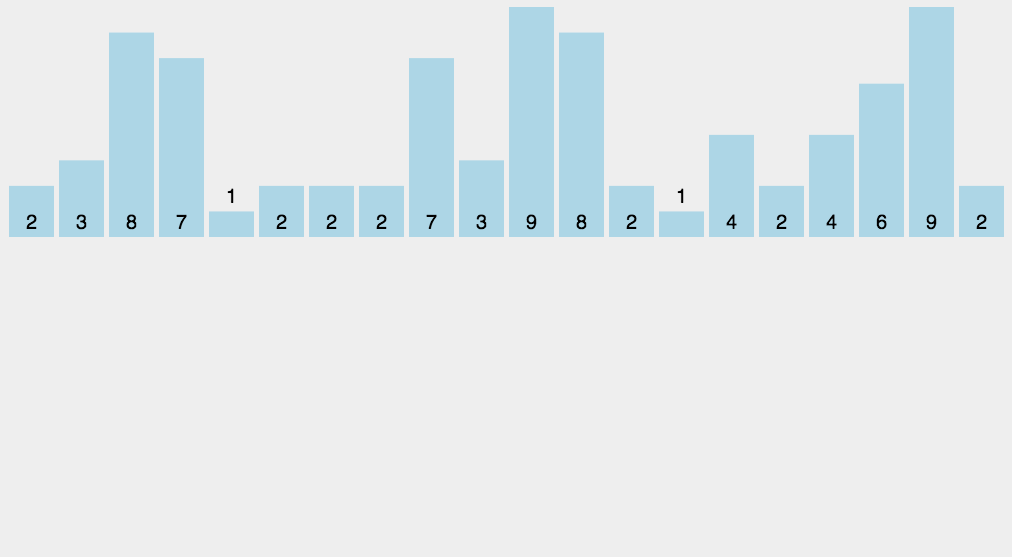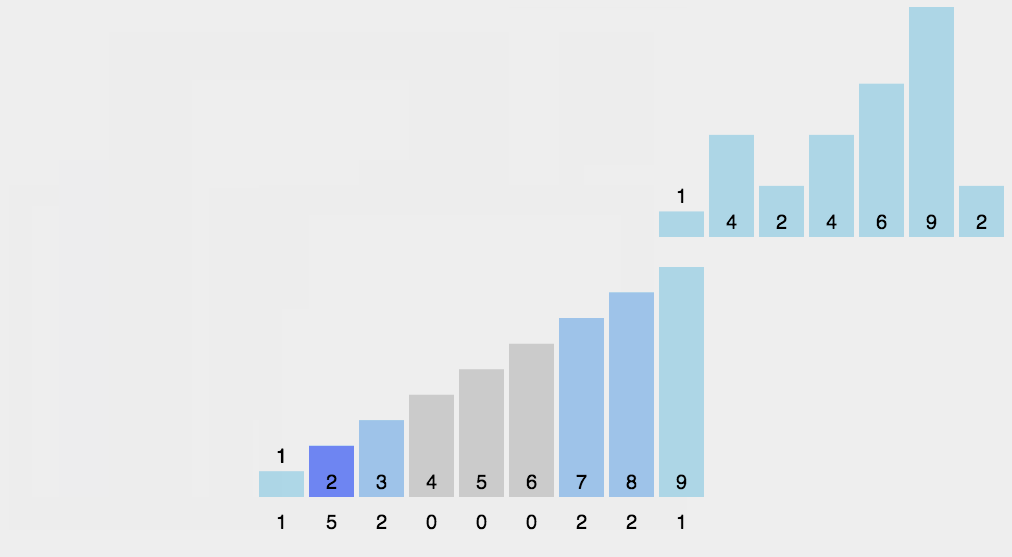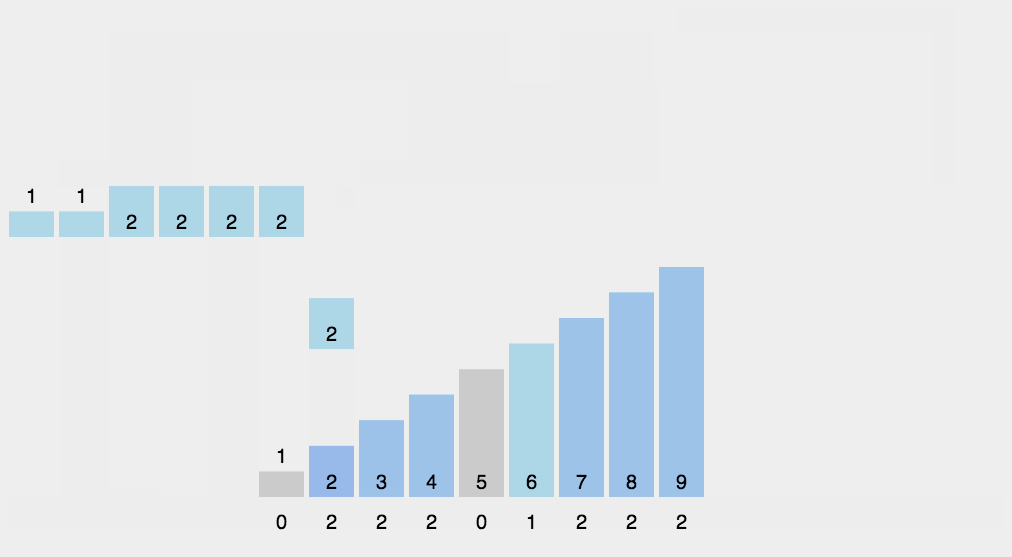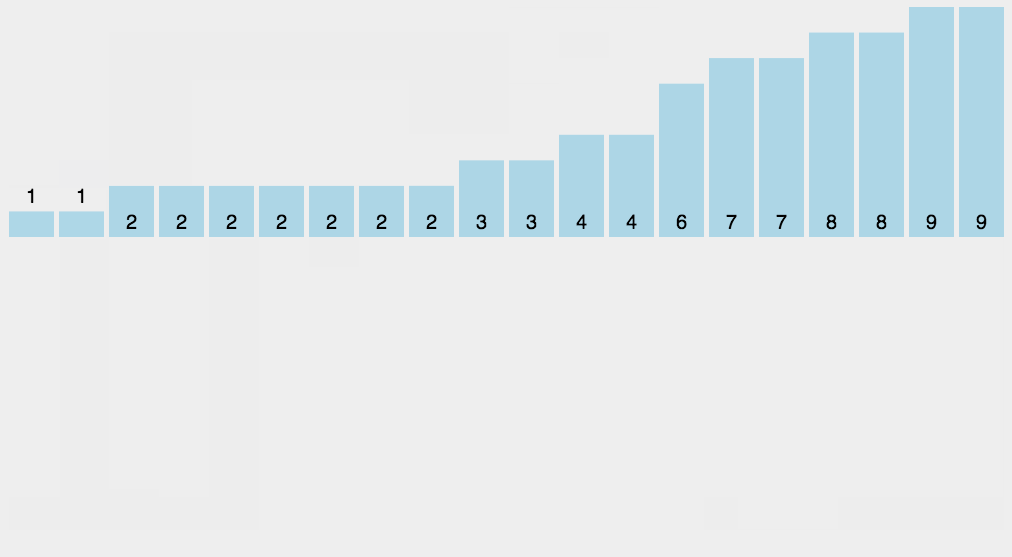
countingsort

代码

def counting_sorted(nums):
	# 计数排序针对非负整数，初始化最大值为-1，也可以设为nums[0]
    maxValue=-1
	for num in nums:
		if num>maxValue:
			maxValue=num
	bucket = [0]*(maxValue+1)
	for num in nums:
		bucket[num]+=1
	index=0
	for i in range(len(bucket)):
		while bucket[i]>0:
			nums[index] = i
			index+=1
			bucket[i]-=1
	return nums

基数排序#

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。

流程

取得数组中的最大数，并取得位数；
从最低位开始取每个位组成 radix 数组；
对 radix 进行计数排序（利用计数排序适用于小范围数的特点）。

radix

代码

def radix_sorted(nums):
	# 基数排序针对非负整数，初始化最大值为-1,也可以设为nums[0]
    maxValue=-1
	for num in nums:
		if num>maxValue:
			maxValue=num 
	# 求最高位数n
	n=len(str(maxValue))
	# 进行n次排序
	for k in range(n):       
		s=[[] for i in range(10)]
		for i in nums:
			s[i//(10**k)%10].append(i)
		nums=[a for b in s for a in b]
	return nums

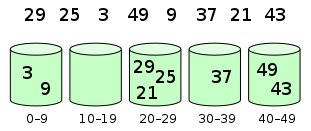
桶排序#

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。桶排序（Bucket sort）的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排）。

流程

设置一个定量的数组当作空桶；
遍历输入数据，并且把数据一个一个放到对应的桶里去；
对每个不是空的桶进行排序；
从不是空的桶里把排好序的数据拼接起来。

bucket1

bucket2

代码

def bucket_sorted(nums):
	if not nums:return nums
	maxValue=nums[0]
	minValue=nums[0]
	for num in nums:
		if num>maxValue:
			maxValue=num 
		elif num<minValue:
			minValue=num
	# 将数据映射到桶中
	bucketSize=100 # 设定桶的大小
	bucketCount=(maxValue-minValue)//bucketSize+1 # 计算桶的数量
	buckets=[[] for _ in range(bucketCount)]
	for num in nums:
		buckets[(num-minValue)//bucketSize].append(num)
	# 对桶内排序，这里使用插入排序，也可以递归桶排序。
	res=[]
	for k in buckets:       
		res=res+insertion_sorted(k)
	return res
# 插入排序
def insertion_sorted(nums):
	size = len(nums)
	for i in range(1,size):
		cur_num=nums[i]
		pre_index=i-1

		while nums[pre_index]>cur_num and pre_index>=0:
			nums[pre_index+1]=nums[pre_index]
			pre_index-=1
		nums[pre_index+1]=cur_num
	return nums

总结#

桶排序、基数排序和计数排序都属于非比较类排序，其中计数排序和基数排序都用到了桶排序的思想。计数排序一共分了 0，1，2, …, maxValue 一共 maxValue + 1 个桶，每个桶表示一个数；而基数排序则分了十个桶，从第一位开始递归桶排序。冒泡排序，选择排序，插入排序都是比较两个数然后交换。堆排序，归并排序，快速排序则是运用了分治的思想。

分类#