贪心算法
一旦一个问题可以通过贪心法来解决,那么贪心法一般是解决这个问题的最好办法。
一、概述#
贪心算法(greedy algorithm),是一种在每一步选择中都采取在当前状态下最好或最优(即最有利)的选择,从而希望导致结果是最好或最优的算法。比如在旅行推销员问题 中,如果旅行员每次都选择最近的城市,那这就是一种贪心算法。
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是局部最优解能决定全局最优解。简单地说,问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
贪心法可以解决一些最优化问题,如:求图中的最小生成树 、求哈夫曼编码 ……对于其他问题,贪心法一般不能得到我们所要求的答案。一旦一个问题可以通过贪心法来解决,那么贪心法一般是解决这个问题的最好办法。由于贪心法的高效性以及其所求得的答案比较接近最优结果,贪心法也可以用作辅助算法或者直接解决一些要求结果不特别精确的问题。
二、流程#
- 创建数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到子问题的局部最优解;
- 把子问题的解局部最优解合成原来解问题的一个解。
三、题解#
回溯算法,动态规划和贪心算法其实是循序渐进的。回溯算法即是暴力的枚举,每一步对所有可能都进行计算,计算到达终点即返回,每一步返回后都要把状态回归到之前的状态。回溯算法的痛点是他有很多重复的计算,解决的办法是引入备忘录,备忘录记录了每一步的结果,这其实就是子问题的最优解,动态规划由此产生。所以使用动态规划时必须要满足无后效性,子问题的解一旦确定,就不再改变,不受在这之后、包含它的更大的问题的求解决策影响。如果一个问题没有重叠子问题,那就只能使用回溯算法,比如 N 皇后问题 。
对于有些问题,我们通过建立数学模型之后明确知道了子问题的最优解,那么就不需要枚举各种情况了。比如有 5 元,2 元和 1 元三种硬币无限个,求用这些硬币兑换 x 元的最少硬币个数。解决这个问题总是先考虑最大面额的硬币,并不需要枚举。但是对于 5 元,4 元和 1 元这三个面额,贪心算法并不能得出最优解。
3.1 加油站#
leetcode 134. 加油站 :在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
- 如果题目有解,该答案即为唯一答案。
- 输入数组均为非空数组,且长度相同。
- 输入数组中的元素均为非负数。
示例:
输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3
这个问题的子问题是从第 i 个加油站出发,到达每个站的油量大于等于 0 ,则返回这个节点。
遍历所有节点,cur记录当前节点油箱内剩余油量,p记录可能的起点。如果cur小于 0 ,那么这个节点包括之前的节点都不可能是起点,将cur置 0 ,p置为下一个节点。
class Solution {
public int canCompleteCircuit(int[] gas, int[] cost) {
int cur = 0, sum = 0, p = 0;
for (int i = 0; i < gas.length; i++) {
cur += gas[i] - cost[i];
sum += gas[i] - cost[i];
if (cur < 0) {
p = i + 1;
cur = 0;
}
}
return sum < 0 ? -1 : p;
}
}
3.2 跳跃游戏 II#
leetcode 45. 跳跃游戏 II :给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
这是典型的可以采用回溯算法的问题,子问题是每一步跳哪个位置,显然回溯算法的时间复杂度非常高。实际上并不需要对每一步仔细推敲,只需要遍历当前步所有位置并求得下一步的最远位置。
class Solution {
public int jump(int[] nums) {
int end = 0, p = 0, i = 0, count = 0;
while (p < nums.length - 1) { // 可达最后就跳出
end = Math.max(end, nums[i] + i);
if (i == p) { // 到达当前布终点
p = end; // 更新终点
count++;
}
i++;
}
return count;
}
}
3.3 分发糖果#
leetcode 135. 分发糖果 :老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻的孩子中,评分高的孩子必须获得更多的糖果。
示例:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
从左到右,从右到左扫描两次数组。
class Solution {
public int candy(int[] ratings) {
int n = ratings.length;
int[] candies = new int[n];
Arrays.fill(candies, 1);
for (int i = 1; i < n; i++) {
if (ratings[i] > ratings[i - 1]) candies[i] = candies[i - 1] + 1;
}
for (int i = n - 2; i >= 0; i--) {
if (ratings[i] > ratings[i + 1])
candies[i] = Math.max(candies[i], candies[i + 1] + 1);
}
int count = 0;
for (int candy : candies) count += candy;
return count;
}
}
3.4 判断子序列#
leetcode 392. 判断子序列 :给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长(长度 ~= 500,000),而 s 是个短字符串(长度 <=100)。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,“ace” 是 “abcde” 的一个子序列,而 “aec” 不是)。
示例:
s = "abc", t = "ahbgdc"
返回 true.
如果是匹配一个较短字符串 s ,对于 s 中每一个字符都优先匹配最开始遇到的,直接扫描一遍 t 即可:
class Solution {
public boolean isSubsequence(String s, String t) {
int i = 0;
for (char ch : s.toCharArray()) {
while (i < t.length() && t.charAt(i) != ch) i++;
i++;
}
return i <= t.length() ? true : false;
}
}
匹配一串字符需要 $O(n)$ ,n 为 t 的长度。如果有大量输入的 S,称作 S1 , S2 , … , Sk 其中 k >= 10 亿,你需要依次检查它们是否为 T 的子序列,这时候处理每一个子串都需要扫描一遍 T 是很费时的。
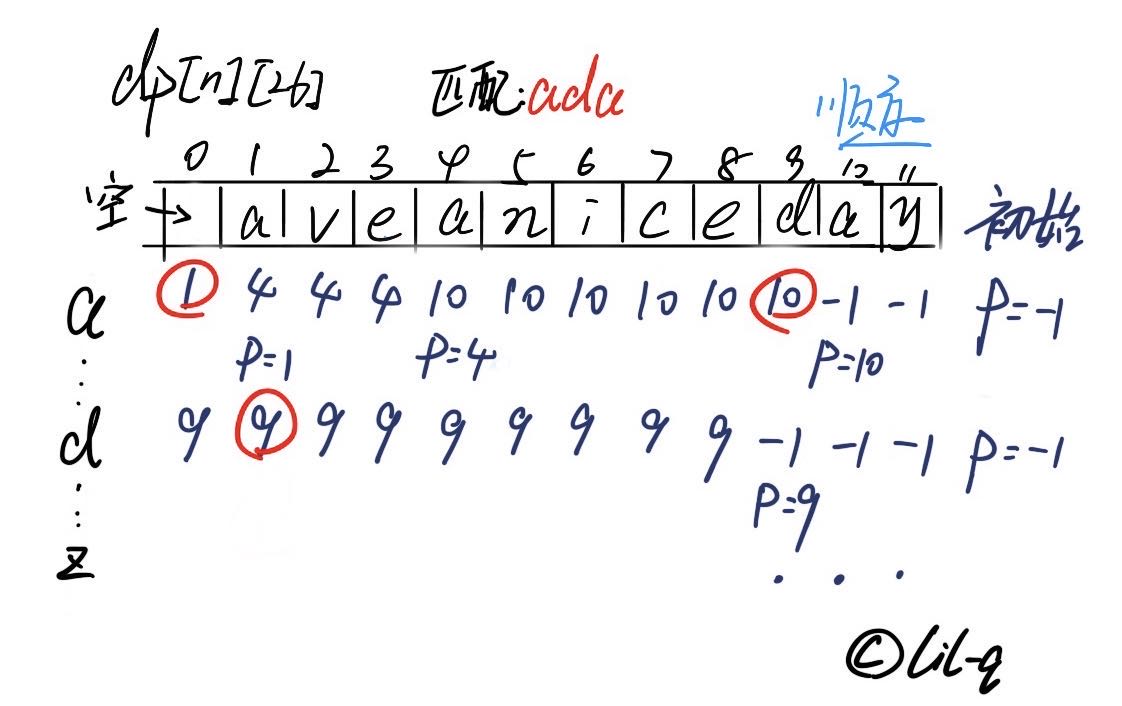
在这种情况下,我们需要在匹配前对 T 做预处理,利用一个二维数组记录每个位置的下一个要匹配的字符的位置,这里的字符是 ‘a’ ~ ‘z’,所以这个数组的大小是 dp[n][26],n 为 T 的长度。那么每处理一个子串只需要扫描一遍 Si 即可,因为在数组的帮助下我们对 T 是“跳跃”扫描的。比如下面匹配 “ada” 的例子,只需要“跳跃”三次。
class Solution {
public boolean isSubsequence(String s, String t) {
t = " " + t; // 开头加一个空字符作为匹配入口
int n = t.length();
int[][] dp = new int[n][26]; // 记录每个位置的下一个ch的位置
for (char ch = 0; ch < 26; ch++) {
int p = -1;
for (int i = n - 1; i >= 0; i--) { // 从后往前记录dp
dp[i][ch] = p;
if (t.charAt(i) == ch + 'a') p = i;
}
}
int i = 0;
for (char ch : s.toCharArray()) {
i = dp[i][ch - 'a'];
if (i == -1) return false;
}
return true;
}
}
3.5 根据身高重建队列#
leetcode 406. 根据身高重建队列 :假设有打乱顺序的一群人站成一个队列。 每个人由一个整数对 (h, k) 表示,其中 h 是这个人的身高,k 是排在这个人前面且身高大于或等于 h 的人数。 编写一个算法来重建这个队列。
示例:
输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]
输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]
优先处理身高高的,这样后续插入矮个子对后排高个儿是没有影响的:
class Solution {
public int[][] reconstructQueue(int[][] people) {
Arrays.sort(people, (p1, p2) -> p2[0] == p1[0] ? p1[1] - p2[1] : p2[0] - p1[0]);
List<int[]> list = new LinkedList<>();
for (int[] p : people) {
list.add(p[1], p);
}
int n = people.length;
return list.toArray(new int[n][2]); // 需要传入同类型新数组
}
}
3.6 按要求补齐数组#
leetcode 330. 按要求补齐数组 :给定一个已排序的正整数数组 nums,和一个正整数 n 。从 [1, n] 区间内选取任意个数字补充到 nums 中,使得 [1, n] 区间内的任何数字都可以用 nums 中某几个数字的和来表示。请输出满足上述要求的最少需要补充的数字个数。
示例:
输入: nums = [1,3], n = 6
输出: 1
解释:
根据 nums 里现有的组合 [1], [3], [1,3],可以得出 1, 3, 4。
现在如果我们将 2 添加到 nums 中, 组合变为: [1], [2], [3], [1,3], [2,3], [1,2,3]。
其和可以表示数字 1, 2, 3, 4, 5, 6,能够覆盖 [1, 6] 区间里所有的数。
所以我们最少需要添加一个数字。
可以用二进制数的思想去考虑这个问题:
class Solution {
public int minPatches(int[] nums, int n) {
int count = 0, i = 0;
long cur = 0; // 注意可能会溢出
while (cur < n) {
if (i == nums.length || cur + 1 < nums[i]) {
cur += cur + 1;
count += 1;
} else {
cur += nums[i];
i++;
}
}
return count;
}
}
3.7 任务调度器#
leetcode 621. 任务调度器 :给定一个用字符数组表示的 CPU 需要执行的任务列表。其中包含使用大写的 A - Z 字母表示的 26 种不同种类的任务。任务可以以任意顺序执行,并且每个任务都可以在 1 个单位时间内执行完。CPU 在任何一个单位时间内都可以执行一个任务,或者在待命状态。然而,两个相同种类的任务之间必须有长度为 n 的冷却时间,因此至少有连续 n 个单位时间内 CPU 在执行不同的任务,或者在待命状态。
示例 :
输入:tasks = ["A","A","A","B","B","B"], n = 2
输出:8
解释:A -> B -> (待命) -> A -> B -> (待命) -> A -> B.
在本示例中,两个相同类型任务之间必须间隔长度为 n = 2 的冷却时间,而执行一个任务只需要一个单位时间,所以中间出现了(待命)状态。
利用一个表格来安排任务,官方题解 给出了很好的解释
class Solution {
public int leastInterval(char[] tasks, int n) {
int[] counter = new int[26];
for (char ch : tasks) counter[ch - 'A']++; // 数组代替Map
Arrays.sort(counter); // 排序
int a = 1;
for (int i = 24; i >= 0; i--) { // 找出并列数量最大的任务有几个
if (counter[i] == counter[i + 1]) a++;
else break;
}
return Math.max(tasks.length, (n + 1) * (counter[25] - 1) + a);
}
}