查并集
查并集的进化之路
一、定义#
并查集是一种树形的数据结构,顾名思义,它用于处理一些不交集的 合并 及 查询 问题。 它支持两种操作:
- 查找(Find):确定某个元素处于哪个子集;
- 合并(Union):将两个子集合并成一个集合。
也就是说,不支持集合的分离、删除。
二、Quick-Find算法#
以下图为例,连通关系为 [(1,2), (0, 1), (0, 3), (4, 7), (5, 6), (5, 7), (7, 8), (8, 9)]。
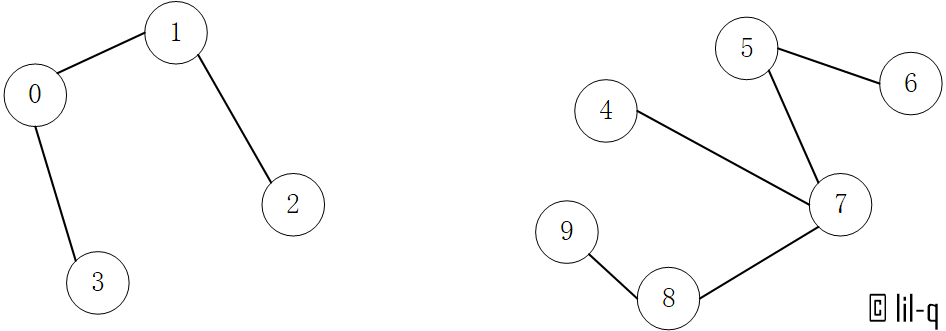
首先初始化所有节点,认为它们属于一个组,因此不连通的节点必然就属于不同的组:
| element | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| group number / id | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
输入 pair(1, 2),则将所有 group number 为 0 和 1 的 element 改为一致(都为 0 或都为 1,这里以较小值为例)。
| element | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| group number / id | 0 | 1 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
输入 pair(0, 1),这里就需要把 element 1 和 element 2 的 group number 都改为 0:
| element | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| group number / id | 0 | 0 | 0 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
正因为每次都需要找到所有的特定 group number 的 element,所以 union 的时间复杂度为 O(N),find 的时间复杂度为 O(1)。N 为 element 的个数,下同。
代码
class QuickFind(object):
id = []
count = 0
def __init__(self, n):
self.count = n
for i in range(n):
self.id.append(i)
def connected(self, p, q):
return self.find(p) == self.find(q)
def find(self, p):
return self.id[p]
def union(self, p, q):
idp = self.find(p)
idq = self.find(q)
if idp != idq:
for i in range(len(self.id)):
if self.id[i] == idq: # 将q所在组内的所有节点的id都设为p的当前id
self.id[i] = idp
self.count -= 1
三、Quick-Union算法#
对于只需要实现查找和合并的并查集,O(n) 的时间复杂度还是太高了,当时间复杂度需要降低到对数级,我们自然想到了树这个数据结构。由于并查集初始化中每一个 element 对于一个 group number,所以可以通过数组中的跳转来实现树的寻找父节点功能。以下图为例,最开始每一个 element 的父节点都是自身,每次查找沿着父节点向上, 直到根节点。每次合并把找到的两个根节点的其中一个设置为另一个的父节点。
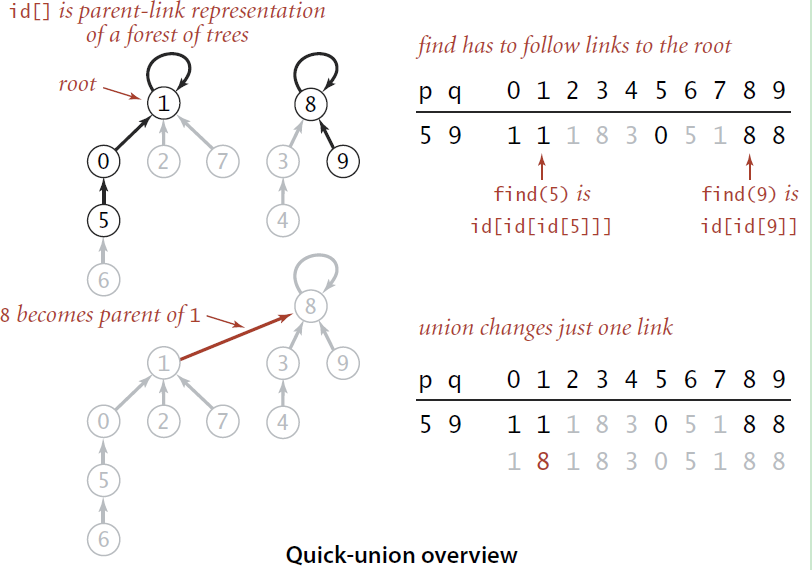
union 和 find 的时间复杂度取决于树的高度。
代码
class QuickUnion(object):
id = []
count = 0
def __init__(self, n):
self.count = n
for i in range(n):
self.id.append(i)
def connected(self, p, q):
return self.find(p) == self.find(q)
def find(self, p):
while (p != self.id[p]):
p = self.id[p]
return p
def union(self, p, q):
root_p = self.find(p)
root_q = self.find(q)
if root_p != root_q:
self.id[root_q] = root_p
self.count -= 1
注意:此时 self.id 存放的不再是每个元素的组别而是父节点。
四、Weighted Quick-Union 算法#
既然采用了树的结构,就有可能出现极端情况,是的树操作的时间复杂度退化成 O(N)。为了避免这种情况,常规方法是使用平衡树,而对于并查集,只需要在 union 时,选择将小的树合并到大树上就可以了。
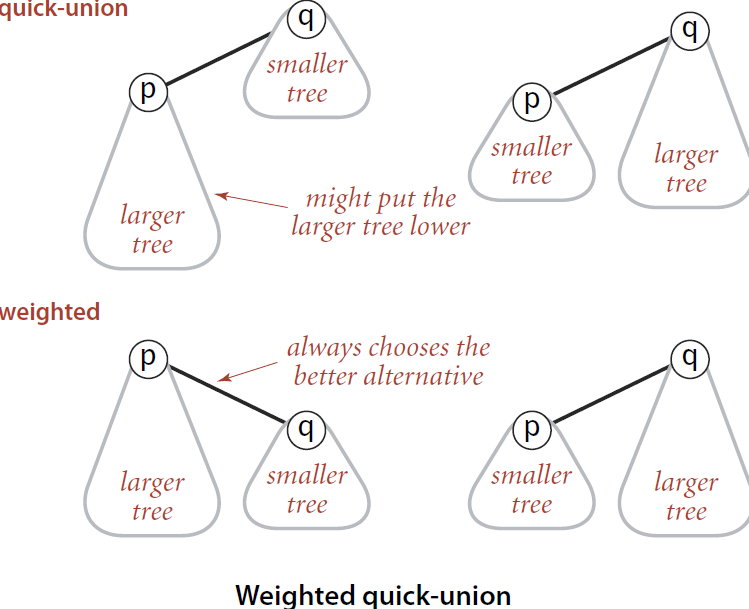
理论上在平衡树合并两个树时,应当用根的高度来衡量两个树的大小,但是这里使用根节点的子孙节点的数量来衡量,union 和 find 的时间复杂度接近于 O(log N)。这是因为这个方法还可以优化,通过路径压缩可以将 union 和 find 的时间复杂度降低至 O(1),而这样做会改变根的高度。
代码
class WeightedQuickUnion(object):
id = []
count = 0
sz = []
def __init__(self, n):
self.count = n
for i in range(n):
self.id.append(i)
self.sz.append(1) # inital size of each tree is 1
def connected(self, p, q):
return self.find(p) == self.find(q)
def find(self, p):
while (p != self.id[p]):
p = self.id[p]
return p
def union(self, p, q):
root_p = self.find(p)
root_q = self.find(q)
if root_p != root_q:
if self.sz[root_p] < self.sz[root_q]:
self.id[root_p] = root_q
self.sz[root_q] += self.sz[root_p]
else:
self.id[root_q] = root_p
self.sz[root_p] += self.sz[root_q]
self.count -=1
输出 self.sz 可以看到 id = 1 和 id = 5 的组别包含了所有元素,id = 4 组中的 (4, 7) 实际上已经移动到 id = 5 组中。
size: [1, 4, 1, 1, 2, 6, 1, 1, 1, 1]
五、Path Compression#
第一种方法是在 find 方法的执行过程中保存所有路过的中间节点到一个数组中,然后在 while 循环结束之后,将这些中间节点的父节点指向根节点。但是这个方法在 find 操作很频繁时会频繁生成中间节点数组,相应的分配销毁的时间自然就上升了。另一种方法是在寻找 q 的根节点的同时不断改变父节点,相当于在寻找根节点的同时,不断地将 q 移动到上一级的节点下,对路径进行了压缩,使整个树结构扁平化。相应的实现如下,实际上只需要在 find 方法中添加一行代码。
def find(self, p):
while (p != self.id[p]):
self.id[p] = self.id[self.id[p]]
p = self.id[p]
return p
这样 self.id 中保存的既是个元素的组别又是各元素的父节点,正因为如此 union 和 find 的时间复杂度降低到了 O(1)。
final parent/id list is 1,1,1,1,5,5,5,5,5,5
六、总结#
随着一步步地深入,我们最终将查并集 union 和 find 的时间复杂度降低到了 O(1)。本文中的四种算法的时间复杂度如下表所示。
| Algorithm | Constructor | Union | Find |
|---|---|---|---|
| Quick-Find | N | O(N) | O(1) |
| Quick-Union | N | Tree height | Tree height |
| Weighted Quick-Union | N | near to O(log N) | near to O(log N) |
| Weighted Quick-Union With Path Compression | N | Very near to O(1) | Very near to O(1) |
需要注意 Path Compression 是将各节点压缩到根节点下,所以 Weighted 仍然有意义。当然如果还需要输出连通路径,这个方法是没办法实现的,需要 BFS 或 DFS 算法来实现。