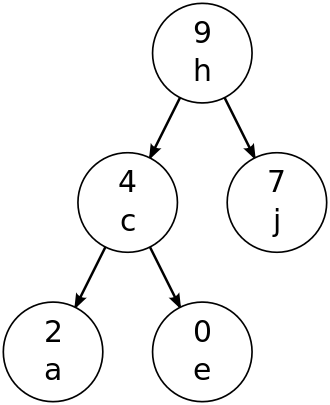
树
之所以叫树是因为他看起来像一棵倒挂的树
一、定义#
树(tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由 n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。它具有以下的特点:
- 每个节点都只有有限个子节点或无子节点;
- 没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)。
术语
- 节点的度(Degree):一个节点含有的子树的个数称为该节点的度;
- 树的度(Degree of tree):一棵树中,最大的节点度称为树的度;
- 叶节点(Leaf):度为零的节点;
- 分支节点(Branch node):度不为零的节点;
- 父节点(Parent):若一个节点含有子节点,则这个节点称为其子节点的父节点;
- 子节点(child):一个节点含有的子树的根节点称为该节点的子节点;
- 兄弟节点(siblings):具有相同父节点的节点互称为兄弟节点;
- 层次(level):从根开始定义起,根为第 1 层,根的子节点为第 2 层,以此类推;
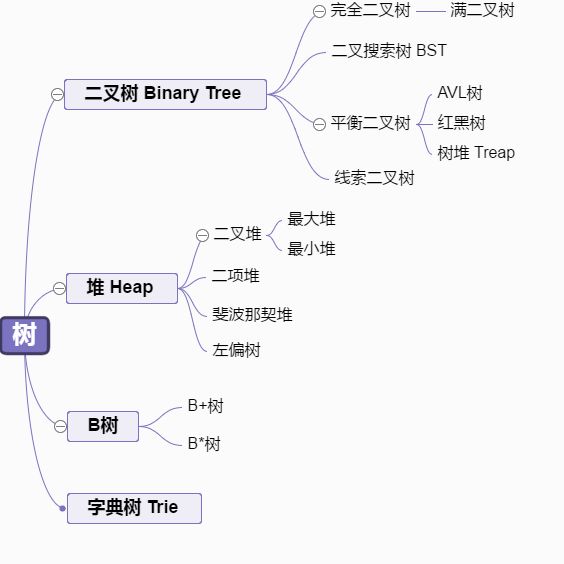
- 深度(depth):对于任意节点 n,n 的深度为从根到 n 的唯一路径长,根的深度为 0;
- 高度(height):对于任意节点 n,n 的高度为从 n 到树叶的最长路径长;
- 节点的祖先(ancestor):从根到该节点所经分支上的所有节点;
- 森林(forest):由 m(m >= 0)棵互不相交的树的集合称为森林。
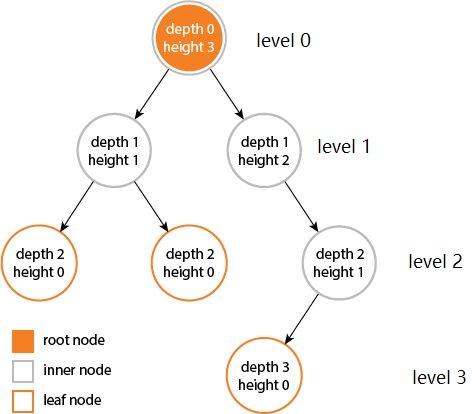
分类
本文将介绍二叉树(Binary tree)、二叉搜索树(Binary search tree)和字典树(Trie)。关于AVL树(AVL tree)、红黑树(Red–black tree)和B树(B-tree),不做深入探讨。
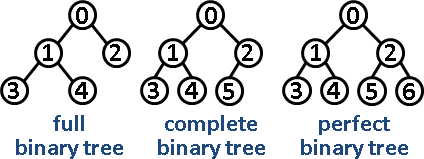
这里区分一下完全二叉树、满二叉树、完美二叉树:
- 完全二叉树:最后一层的叶子节点均需在最左边;
- 满二叉树:满足完全二叉树性质,树中除了叶子节点,每个节点都有两个子节点;
- 完美二叉树:满足满二叉树性质,树的叶子节点铺满最后一层
二、二叉树#
二叉树(Binary tree)是每个节点最多只有两个分支(即不存在分支度大于 2 的节点)的树结构。通常分支被称作 “左子树” 或 “右子树”。二叉树的分支具有左右次序,不能随意颠倒。
# 建一个单节点
class Node(object):
def __init__(self, value):
self.val = value
self.left = None #左节点
self.right = None #右节点
'''
# 建一个二叉树
# 1
# / \
# 2 3
# / \ / \
# 4 5 6 7
'''
root = Node(1)
stack = [root]
value = 2
for i in range(3):
cur = stack.pop(0)
cur.left = Node(value)
stack.append(cur.left)
value += 1
cur.right = Node(value)
stack.append(cur.right)
value += 1
2.1 二叉树的遍历#
二叉树的遍历有前序遍历、中序遍历、后序遍历和层序遍历等,可用迭代和递归两个方法。
1. 前序遍历
递归
def preorderTraversal(root):
if not root:
return
print(root.val, end = ' ')
preorderTraversal(root.left)
preorderTraversal(root.right)
迭代
# 方法一
def preorderTraversalIter(root):
if not root:
return res
stack = [root]
while stack:
node = stack.pop()
print(node.val, end = ' ')
if node.right:
stack.append(node.right)
if node.left:
stack.append(node.left)
# 方法二
def preorderTraversalIter(root):
if not root:
return res
stack = []
while root or stack:
while root:
stack.append(root)
print(root.val, end = ' ')
root=root.left
root=stack.pop()
root=root.right
2. 中序遍历
递归
def inorderTraversal(root):
if not root:
return
inorderTraversal(root.left)
print(root.val)
inorderTraversal(root.right)
迭代
def inorderTraversalIter(root):
if not root:
return res
stack = []
while root or stack:
while root:
stack.append(root)
root=root.left
root=stack.pop()
print(root.val, end = ' ')
root=root.right
3. 后序遍历
递归
def postorderTraversal(root):
if not root:
return
postorderTraversal(root.left)
postorderTraversal(root.right)
print(root.val)
迭代
比较 tricky 的办法是吧后序遍历转变成中右左遍历的倒序,代码如下
# 方法一
def postorderTraversalIter(root):
res = []
if not root:
return res
stack = [root]
while stack:
node = stack.pop()
if node.left :
stack.append(node.left)
if node.right:
stack.append(node.right)
res.append(node.val)
return res[::-1]
# 方法二
def postorderTraversalIter(root):
res = []
if not root:
return res
stack = []
while root or stack:
while root:
stack.append(root)
res.append(root.val)
root = root.right
root = stack.pop()
root = root.left
return res[::-1]
4. 层序遍历
def levelOrderTraversal(root):
# 使用列表模拟先进先出队列queue
queue = [root]
while queue:
node = queue.pop(0)
if node.left :
queue.append(node.left)
if node.right:
queue.append(node.right)
print(node.val, end = ' ')
输出
前序遍历_递归:
1 2 4 5 3 6 7
前序遍历_迭代:
1 2 4 5 3 6 7
中序遍历_递归:
4 2 5 1 6 3 7
中序遍历_迭代:
4 2 5 1 6 3 7
后序遍历_递归:
4 5 2 6 7 3 1
后序遍历_迭代:
4 5 2 6 7 3 1
层序遍历:
1 2 3 4 5 6 7
2.2 二叉树的序列化#
「序列化」(serialization),指的是把复杂的数据结构转化为线性结构,以方便存储的过程。序列化得到的线性结构必须能重建出原有的结构,才有意义。
仅使用一种遍历的序列化方法
这是最常见的序列化方法。可以采用的遍历顺序包括先序、后序、层序。在遍历时,要把空指针也包含在遍历的结果中。例如,对下图的二叉树,进行先序、后序、层序遍历的结果分别为 12##3#4##、##2###431、123###4##(# 表示空指针)。
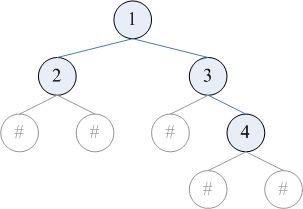
def reconstruct(root):
if not root:
return res
stack = [root]
while stack:
node = stack.pop()
print(node.val, end=' ')
if node.right:
stack.append(node.right)
else:
print('#', end = ' ')
if node.left:
stack.append(node.left)
else:
print('#', end = ' ')
而仅根据(带空指针的)中序遍历,是不能重建二叉树的。比如,上面这棵树的中序遍历为 #2#1#3#4#。事实上可以证明,任何一棵二叉树的中序遍历结果,都会是空指针与树中结点交替出现的形式,所以空指针没有提供任何额外的信息。原文
三、二叉搜索树#
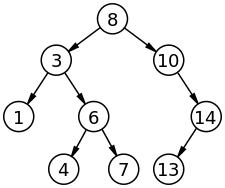
二叉查找树(Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
- 没有键值相等的节点。
空间复杂度:O(n)。
时间复杂度:
| 算法 | 平均 | 最差 |
|---|---|---|
| 搜索 | O(log n) | O(n) |
| 插入 | O(log n) | O(n) |
| 删除 | O(log n) | O(n) |
3.1 插入节点#
- 若 b 是空树,则将
node所指节点作为根节点插入,否则; - 若
node.val等于 b 的根节点的数据域之值,则返回,否则; - 若
node.val小于 b 的根节点的数据域之值,则把s所指节点插入到左子树中,否则; - 把
node所指节点插入到右子树中。
新插入节点总是叶子节点,所以数字组成相同但是排序不同的序列所构造的二叉搜索树其实是不同的。但是序列化(见后文)的结果是一致的。
3.2 查找节点#
- 若 b 是空树,则搜索失败,否则:
- 若 x 等于 b 的根节点的数据域之值,则查找成功;否则:
- 若 x 小于 b 的根节点的数据域之值,则搜索左子树;否则:
- 查找右子树
3.3 删除节点#
这里给出递归的方式。递归的好处在于不用考虑寻找父节点以及待删除结点到底是父节点的左子节点还是右子节点(leetcode 450 非递归,较为复杂的解法 )。
在二叉查找树删去一个结点,分三种情况讨论:
- 若待删除结点 p 为叶子结点,即 PL(左子树)和 PR(右子树)均为空树。由于删去叶子结点不破坏整棵树的结构,则只需修改其双亲结点的指针即可。
- 若待删除结点只有左子树 PL 或右子树 PR,此时只要令 PL 或 PR 直接成为其双亲结点 f 的左子树(当 p 是左子树)或右子树(当 p 是右子树)即可,作此修改也不破坏二叉查找树的特性。
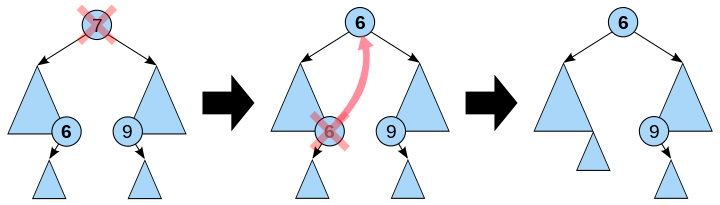
- 若 p 结点的左子树和右子树均不空。在删去 p 之后,为保持其它元素之间的相对位置不变,可按中序遍历保持有序进行调整,可以有两种做法:其一是令 p 的左子树为 f 的左/右(依 p 是 f 的左子树还是右子树而定)子树,s 为 p 左子树的最右下的结点,而 p 的右子树为 s 的右子树;其二是令 p 的直接前驱(in-order predecessor)或直接后继(in-order successor)替代 p,然后再从二叉查找树中删去它的直接前驱(或直接后继)。
四、字典树#
Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
class Trie:
# 初始化
def __init__(self):
self.lookup = {}
def insert(self, word):
tree = self.lookup
for a in word:
if a not in tree:
tree[a] = {}
tree = tree[a]
# 单词结束标志
tree["#"] = "#"
def search(self, word):
tree = self.lookup
for a in word:
if a not in tree:
return False
tree = tree[a]
if "#" in tree:
return True
return False
def startsWith(self, prefix):
tree = self.lookup
for a in prefix:
if a not in tree:
return False
tree = tree[a]
return True
五、B 树 & B+ 树#
B 树(B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。B 树,概括来说是一个一般化的二叉查找树(binary search tree)一个节点可以拥有 2 个以上的子节点。与自平衡二叉查找树不同,B树适用于读写相对大的数据块的存储系统,例如磁盘。B 树减少定位记录时所经历的中间过程,从而加快存取速度。B 树这种数据结构可以用来描述外部存储。这种数据结构常被应用在数据库和文件系统的实现上。
B+ 树是一种树数据结构,通常用于数据库和操作系统的文件系统中。B+ 树的特点是能够保持数据稳定有序,其插入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入,这与二叉树恰好相反。
B+ 树与 B 树最大的不同是内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
请参考这篇文章
六、AVL 树#
AVL 树是最早被发明的自平衡二叉查找树。在 AVL 树中,任一节点对应的两棵子树的最大高度差为 1,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(log n)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。
节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
AVL 树的基本操作一般涉及运作同在不平衡的二叉查找树所运作的同样的算法。但是要进行预先或随后做一次或多次所谓的 “AVL 旋转”。
七、红黑树#
在理解红黑树之前需要对 2-3-4 树有一定的了解,2-3-4 树在计算机科学中是阶为 4 的 B 树。大体上同 B 树一样,2-3-4 树是可以用做字典的一种自平衡数据结构。它可以在 O(log n) 时间内查找、插入和删除,这里的 n 是树中元素的数目。
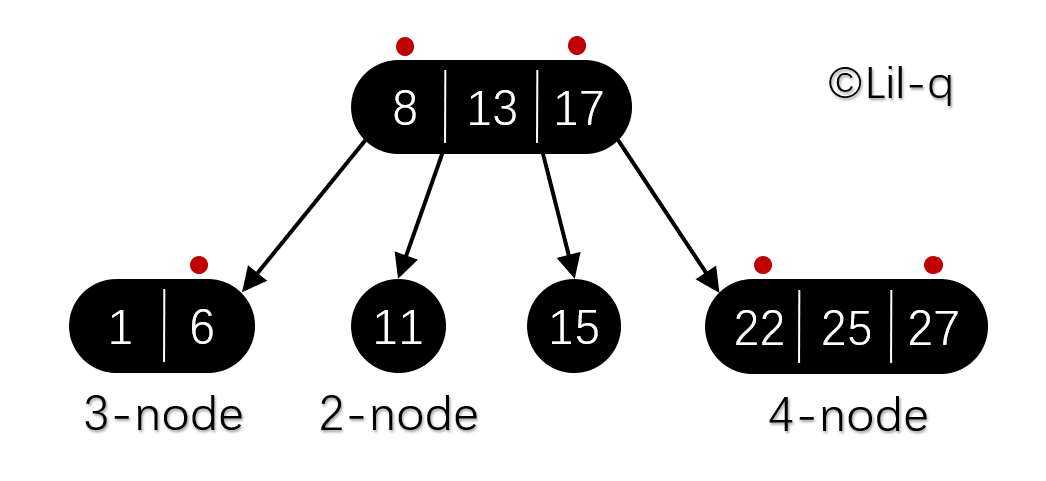
2-3-4 树在多数编程语言中实现起来相对困难,因为在树上的操作涉及大量的特殊情况。红黑树实现起来更简单一些,所以可以用它来替代。注意上图(叶子节点未画出)中用红点标记的位置,与下图红黑树对比就能大概了解 2-3-4 树转换成红黑树的过程。
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求:
- 节点是红色或黑色。
- 根是黑色。
- 所有叶子都是黑色(叶子是 NIL 节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面是一个具体的红黑树的图例:

操作有变色,左旋,右旋。
红黑树 & 平衡二叉树#
红黑树本质上是 2-3-4 树将 3-节点 和 4-节点又转换成 2-节点后形成的二叉搜索树。3-节点 和 4-节点转换后是不平衡的,这就导致了红黑树并不像平衡二叉树那样严格平衡;不过由于 2-3-4 树本身具备的自平衡特性,红黑树的深度与平衡二叉树的差距并不大。查询效率红黑树稍差于平衡二叉树。
对于插入和删除操作,不管是红黑树还是平衡二叉树,旋转操作的复杂度都是 O(1) 且两者维护一次平衡最差情况下都需要 O(log n) 的时间复杂度,但是普遍情况下由于红黑树对于平衡的不严格要求,其旋转的次数要少于平衡二叉树,插入与删除的效率略高于平衡二叉树。
总体上,红黑树的性能优于平衡二叉树,其优势本质上是用空间换时间。
八、树堆#
树堆(Treap)是二叉排序树(Binary Sort Tree)与堆(Heap)结合产生的一种拥有堆性质的二叉排序树。
但是这里要注意两点,第一点是 Treap 和二叉堆有一点不同,就是二叉堆必须是完全二叉树,而 Treap 并不一定是;第二点是 Treap 并不严格满足平衡二叉排序树(AVL树)的要求,即树堆中每个节点的左右子树高度之差的绝对值可能会超过 1,只是近似满足平衡二叉排序树的性质。
Treap 每个节点记录两个数据,一个是键值,一个是随机附加的优先级,Treap 在以关键码构成二叉排序树的同时,又以结点优先级形成最大堆和最小堆。所以 Treap 必须满足这两个性质,一是二叉排序树的性质,二是堆的性质。如下图,即为一个树堆。